Índice | III. Probabilidade | V. Exercícios

IV. Modelos de Probabilidade discretos e contínuos

Parte 8 de 78

Modelos de probabilidade discretos

2.1 – Função massa de probabilidade

Atendendo a que a variável aleatória discreta associa números aos resultados de uma experiência, em vez de falarmos nas probabilidades dos acontecimentos elementares (resultados), podemos falar nas probabilidades dos valores que a variável aleatória assume.

À função que dá a probabilidade associada a cada valor numérico, que a v.a. assume, chamamos
distribuição de probabilidade ou função massa de probabilidade (f.m.p).

Uma variável aleatória X, discreta, fica perfeitamente identificada pela sua f.m.p., isto é, pelos valores x_i que assume e pelas probabilidades de assumir esses valores:

p_i = P(X = x_i)

Atendendo à definição de probabilidade, é imediato que:

a) 0 ≤ p_i ≤ 1 para cada i
b) 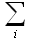p_i = 1

fPartilhar

Tweet